
基于Pregel模型的大规模分布式子图枚举算法
子图枚举算法,作为图分析计算中的一种基本算法,在生物化学、生态学以及生物信息学中有着广泛的应用。例如:分子式之间的同构查找、社交网络中的频繁结构共现和描述社会网络的演变等。当前存在的众多分布式子图枚举算法(PSgL、TwiTwigJoin以及SEED等)会通过网络传输大量的中间结果。本算法从相似中间结果压缩传输角度探讨分布式子图枚举算法,提出一种更低网络传输量、更高效的分布式子图枚举算法。
子图枚举(Subgraph isomorphism)算法的定义是:给定一张查询图和一张数据图,在数据图中查找与查询图同构的所有子图的算法。在本问题中,查询图是一张无方向的(undirected)、无标签的(unlabeled)的全连通图;数据图是一张无方向的(undirected)、无标签的(unlabeled)的图。
当数据图的规模越来越大,中间结果会越来越多,单机的子图枚举算法不能在可接受的时间内完成子图枚举任务。如果要解决大规模数据图下的子图枚举问题,必须使用分布式框架来解决。因此近些年对子图枚举算法的研究工作都转向了关注分布式子图枚举算法的研究。
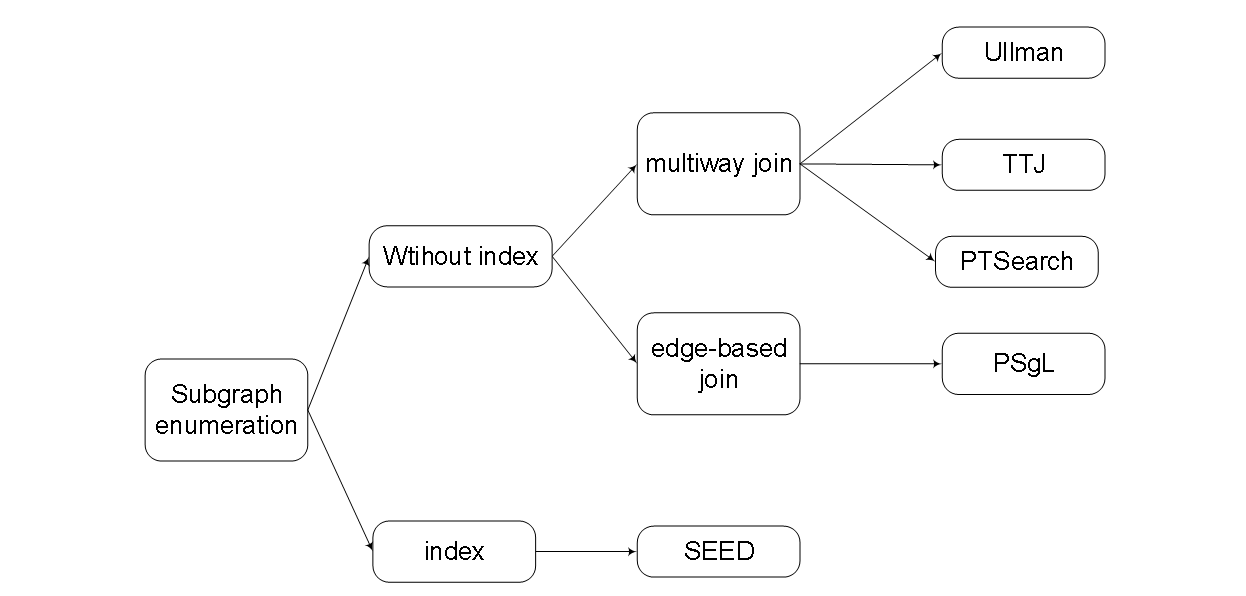
图2-1 分布式子图枚举算法分类
图2-1总结分类了目前的分布式子图枚举算法。当前的分布式的子图枚举算法可以分为两大类:
- 第一类是不使用附加索引结构的分布式子图枚举算法。该分类下的所有算法都仅基于数据图的邻接表信息来完成,适用于数据图和查询图经常变化的情况。Ullman、TwinTwigJoin以及PSgL是其中的代表性算法。
- 第二类是使用索引结构的分布式子图枚举算法。该类算法除了使用基本的数据图邻接表的信息外,还需要通过预处理过程增加额外的索引结构来提高子图枚举算法的效率。这种分布式子图枚举算法适用于数据图更新较少,查询图经常变化的情况。SEED算法是其中的代表性算法。
本算法在详细研究Ullman、PSgL以及TwinTwigJoin算法的基础上认为,目前分布式子图枚举算法可以在两个方面进行改进。首先,TwinTwigJoin限制了star结构为只有一条边或者两条边,导致查询轮数过多,存在进一步优化的空间。其次,TwinTwigJoin算法每次的中间匹配结果还是会全部通过网络进行发送,即使将Star的边数限制到了两条,但发送数量依然很大。
本工作提出了一种新的分布式子图枚举算法PTSearch,其利用中间数据的压缩传输原理,降低了分布式子图枚举算法的网络通信量,取得了更好的性能。
为了实现上述目标,PTSearch算法将分布式子图枚举过程分成了以下三个步骤:查询分解、查询部分匹配结果、展开部分匹配结果。PTSearch算法的整体流程如图3-1所示。
图3-1 PTSearch算法整体设计
本文使用Apache Spark作为PTSearch算法的底层分布式系统,使用GraphX Pregel实现PTSearch算法的部分匹配结果查询部分,使用Redis实现分布式的内存数据存储查询,使用Caffeine作为本地Cache缓存管理库,核心代码使用Scala和Java两种语言混合编程的方式来完成。

图3-2 PTSearch整体框架图
PTSearch算法在分布式环境下实现的整体系统架构如图3-2所示。假设分布式环境中一共有五台机器,分别为Master、Worker1、Worker2、Worker3以及Worker4。图3-2最右边表示在四个Worker上构建的分布式Redis内存数据库,为PTSearch算法中数据图的邻接表存储提供支持。在每一个Worker节点上,同时拥有一个由Caffeine管理的本地Cache,用来缓存从Redis中读取到的数据图邻接表数据。
本算法的核心数据结构Gptr,每个Gptr表示查询树上的一颗子树subi在数据图上的一组匹配结果。Gptr是一种压缩表示,一个Gptr代表了一组的部分匹配结果。在一个Gptr中,查询子树上的每个内部节点(即非叶子节点)都被映射到数据图中的一个顶点,而该子树的每一个叶子节点都被映射到了数据图中的一个顶点的邻接表。
图4-1 Gptr示例图
本算法分为三个部分:查询分解、部分结果查找和展开最终匹配结果。
- 查询分解:将查询图的每个顶点的度数作为该顶点的权重。通过多轮迭代完成查询树生成。具体如图4-2所示。
- 部分匹配结果查找:基于GraphX Pregel模型,通过每轮的迭代从查询图叶子结点开始匹配,直到根节点匹配为止。具体匹配过程如图4-3所示。在d5顶点上匹配以t3为根节点的子树并向其邻接点发送匹配结果,直到在d1上匹配以t1为根节点的查询树,匹配完成。
- 展开最终匹配结果:这个部分将部分匹配结果展开成最终匹配结果,并判断最终匹配结果是否符合正确性的验证条件。

图4-2 查询分解示意图
图4-3 基于GraphX Pregel的示例说明

图4-4 RDD转换图
如图6-3所示,PTSearch算法对于VertexRDD使用flapMap操作,从每个数据图的顶点属性中提取出可以展开的所有Gptr。接着,使用mapPartition操作,对RDD1中的每个分区内的Gptr进行批量地展开,得到所有有效的完全匹配结果。图6-3给出了展开部分匹配结果的整个过程。
本算法在一个拥有17个节点的集群环境下进行所有实验。该集群拥有1个主节点和16个从节点。其中jdk使用jdk 1.8.0_101,Hadoop采用Hadoop-2.7.1,Spark采用Spark2.0.2,Redis采用Redis2.7.2,Caffeine采用Caffeine2.3.5。
实验中一共用到了7个查询图,如图5-1所示。查询图下方是该查询图的自同构信息。
图5-1实验用查询图
实验中一共用到了四张数据图,所有数据图来源于斯坦福大学SNAP数据库[40],如表5-2所示。
表5-2 数据图的信息表
PTSearch算法同时提供了通用代码和针对特性查询图的特定代码两个版本。在查询图性能测试实验中,其中PTSearch算法是通用型的实验结果,PTSearch-O是特定型算法的实验结果。
图5-2给出了查询图Q1到查询图Q7在数据图USPatents上的查询耗时的实验结果,图5-3给出了查询图Q1到查询图Q7在数据图USPatents上的网络通信量性能测试的结果。
图5-2 USPatents上的查询耗时实验结果
图5-3 USPatents上的数据传输量试验
在USPatents数据图上,PSgL只能处理较为简单的图,并且其网络开销非常大。TwinTwigJoin可以处理较为复杂的图,并且具有较好的性能。PTSearch拥有最少的网络传输量,并且在通用型的框架上优于PSgL算法,在特定查询图的框架上优于TwinTwigJoin算法。
PTSearch算法在集群节点上的扩展性实验。
图5-4 集群节点扩展性实验结果
图5-4展示了PTSearch算法的机器可扩展性实验结果。在USPatents数据图上,使用查询图Q6、Q7进行子图枚举任务,当Spark的Executor机器数量从6台增长为16台时,Q6、Q7的查询时间均表现出了线性的节点扩展性,说明PTSearch算法具有良好的机器可扩展性。
子图枚举算法是图算法中非常重要的一个算法,它具有计算复杂度高、中间结果数量多等特点。但是,现有方法并没有很好地解决子图枚举中间结果数量爆炸的问题,尤其是在分布式环境下,大量的中间结果通过网络传输,极大地影响了分布式子图枚举算法的性能。本文针对分布式子图枚举算法中中间结果量过大的问题,给出了一个新的解决思路,极大地减少了分布式子图枚举算法中间结果的数量,提升了分布式子图枚举算法的性能。